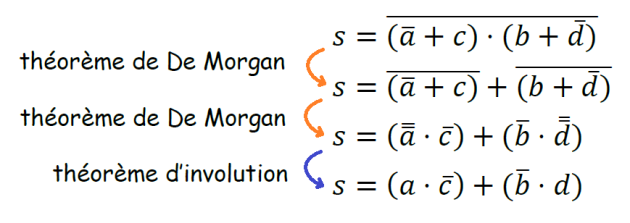
Théorèmes de De Morgan
Définition :
Théorème 1 | Théorème 2 |
|---|---|
\(\overline{a+b} = \bar{a} . \bar{b}\) | \(\overline{a . b} = \bar{a} + \bar{b}\) |
Le complément d'une somme est égal au produit de chacun de ses termes complémentés. | Le complément d'un produit est égal à la somme de chacun de ses termes complémentés. |
Remarque :
Ces théorèmes sont très utilisés pour simplifier les équations logiques.
Remarque :
Ces théorèmes peuvent être généralisables à n variables.
\(\overline{a+b+c+d} = \bar{a} . \bar{b} . \bar{c} . \bar{d}\) | \(\overline{a . b . c . d} = \bar{a} + \bar{b} + \bar{c} + \bar{d}\) |